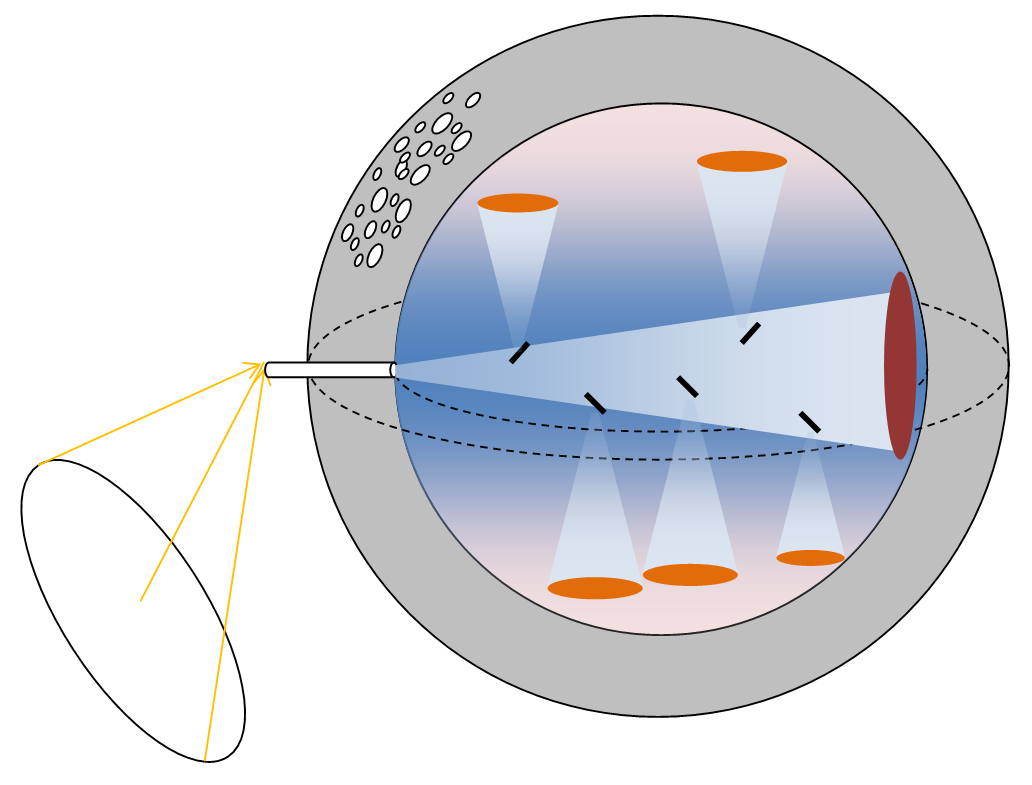
To begin with, I must return to the basic state equation that governs a gravity balloon.
$$ P = \frac{2}{3} \pi \rho^2 G t^2 \frac{\left(3R^2 + 3 R t + t^2\right)}{(R+t)^2} $$
This relates 3 variables, pressure, density, and radius. You need to draw the parallel between volume and the inner radius. Plus, there's somewhat of a 4th variable, which is the total mass of the structure, which can be substituted in and out (numerically usually) with the shell thickness, t. In the process of inflating an asteroid to make a habit the rock mass is constant. Really, you could say this equation is dual to the ideal gas law, in that combining the two fully determines the inner radius (and all other parameters).
Now, given that we have this relationship and methods for solving it, the number of humans that an asteroid or collection of asteroids can house depends on two factors:
- how much space you require per person
- how low of a pressure is okay
For the other limit, the amount of space to comfortably house a human, the numbers are much more ambiguous. On the one hand, we can compare this to other space stations, so I looked up the crew and volume of the International Space Station (ISS), getting a volume per person in cubic meters. We would want more volume than this, but it is an instructive lower bound. For the upper bound, we can look to Earth itself. How much atmosphere do we have per person? That's not a straight-forward question because we all live at different pressures, but with a reductionist goal, I simply divide the mass of Earth's atmosphere by the sea-level density. That gives the volume you would expect if you made a giant balloon of with all Earth's atmosphere and compressed it to sea-level pressure. Obviously this is an overshoot, but that's good, because we now have a clear overshoot and undershoot. These are different by roughly a factor of a million, so I introduced a middle-range number that's the square root of those two numbers multiplied. It's fairly arbitrary, but as far as I can guess, it's probably the best shot at a comfortable volume requirement for people. A 62 meter cube is awfully big, but we should consider that plants and other life would be important as well.
| ISS | Geometric Mean | Earth | |
|---|---|---|---|
| V (km3) per person | 0.0000001 | 0.000237847 | 0.565714286 |
| V (km3) for all humans | 700 | 1.7E+06 | 4.0E+09 |
| Side length (m) | 4.6 | 62.0 | 827.1 |
Unfortunately, I don't expect that I'll do better than a factor of a million. I can get all kinds of (also subjective) numbers for population density per area, but there's no clear idea of the ideal population density of humans per unit volume. In order to appreciate the full weight of the problem, it's useful to consider both extremes.
The one piece of information still missing is a list of existing asteroids. This would be complicated (though not impossible) to do one-by-one, so I'm using a size distribution function instead. The data to do this is very widely published, and I opted to simply use the size distribution list from Wikipedia. The table there gives a cumulative distribution. That is, the number of asteroids above so-and-so diameter. Effectively, a cumulative distribution function (CDF). I obtained a simple power distribution for the data.
Now that we have the CDF, we can also obtain the PDF. Of course, it is the derivative of the former, but since the CDF counts from largest (starting with Ceres) to the Nth asteroid, it's the PDF is the negative of the derivative. This is simply an artifact of how the counting is done.
$$ \text{CDF} = N(>D) = \left( 1.77 \times 10^6 \right) D^{-2.12} \\ \text{PDF} = \frac{dN}{dD} = \left( 3.76 \times 10^6 \right) D^{-3.12} $$
The data was limited to sizes that I already know would be usable as gravity balloons to get the best possible numbers. The exponent is somewhat consistent with other studies on the subject, which found an exponent of -4 (for the PDF) for the large asteroids. I will still use my above number since I know for a fact that it reproduces the numbers I want in this narrow range. With this, all of the information is there to find how many asteroids it would take to house all the human population given some pressure and volume requirement.
The form of the proposal is then to start with the smallest asteroids that is large enough to contain the desired internal pressure, "inflate" that asteroid to a very small volume, then move onto the next one. This next one is larger and thus, we will be able to inflate to a larger inner volume. This continues up the size scale of asteroids until the sum of the internal volumes of all the inflated asteroids comes out to the volume requirement. Density is required for these calculations. In previous posts I assumed a density of 1300 kg/m3, but here I'm changing that to 2000 kg/m3. Reason being that larger asteroids tend to have more volume, and the 1300 number was only a conservatively low number for fairly small asteroids.
On the subject of density, we frankly have no good idea of how dense these asteroids are on the whole. Generally speaking, the measurements of size come from back-calculations from the amount of light we get from the objects. This light does fairly faithfully represent the surface it exposes to space, and that says nothing at all about density. Because of this, we know diameters with much better certainty than what we know mass. For much larger bodies, there is another method for calculating mass, which is to observe their gravitational interactions. This method is completely impractical for the 5,000-some asteroids contained in the set that I'm interested in. It probably wouldn't be possible to employ the method even if the resources were there to do it on one, and doing it for a large number of the asteroids is even more impossible Given that, asteroid density will remain a very major source of uncertainty in all this writing. There isn't a clear basis to employ the figure of 2000 kg/m3 for the density of the set, but the densities are sporadic in the first place. I would prefer to just avoid multivariate PDF integration for the time being. There is certainly room for someone to write an academic paper about reasonable expectations for the full size and density distribution among asteroids. I've found myself at the practical limit of this research so that's my justification for using this generally representative number. It's possible to test the method with different densities and it changes within possibly an order of magnitude with a reasonable density range.
A fun way to give the answer to this query is to say "to get a pressure of 1 atmosphere you need to use asteroids A to Z", meaning that you would need to use all asteroids with sizes between those two candidates. Because of that, I'm quoting a reference asteroid to get the central pressure with no inflated volume (that is the "A"), and then an example asteroid for every volume case (that is the "Z"). Here are the numbers for the two different pressures.
| Case | Cumulative Volume Goal | D (km) | M (kg) | Inflated D (km) | Number Used | Nth Asteroid | Uninflated Pressure (atm) |
|---|---|---|---|---|---|---|---|
| starting size | 0 | 26.9 | 2.04E+16 | 0.0 | - | 277 Elvira | 1.00 |
| ISS | 700 | 28.3 | 2.37E+16 | 2.6 | 162 | 625 Xenia | 1.10 |
| Geometric Mean | 1.66E+06 | 42.8 | 8.21E+16 | 26.4 | 997 | 132 Aethra | 2.53 |
| Earth | 3.96E+09 | 241.4 | 1.47E+19 | 537.4 | 1,639 | 65 Cybele | 80.38 |
| Case | Cumulative Volume Goal | D (km) | M (kg) | Inflated D (km) | Number Used | Nth Asteroid | Uninflated Pressure (atm) |
|---|---|---|---|---|---|---|---|
| starting size | 0 | 15.7 | 4.05E+15 | 0.0 | - | 518 Halawe | 0.34 |
| ISS | 700 | 16.5 | 4.74E+15 | 1.6 | 508 | 433 Eros | 0.38 |
| Geometric Mean | 1.66E+06 | 26.7 | 1.99E+16 | 18.2 | 3,329 | 274 Philagoria | 0.98 |
| Earth | 3.96E+09 | 169.8 | 5.13E+18 | 417.6 | 5,152 | 54 Alexandra | 39.79 |
For example, in order to get an atmosphere volume equal to that of Earth at sea-level pressure, you would need to inflate all the asteroids larger than Elvira and smaller than Cybele (and possibly include those two as well). The value of this observation is that it shows that there is plenty of availability of asteroid material with which to make gravity balloon habitats. In fact, it's not hard to see at all how this approach could easily house more people than all the terrestrial environments in the solar system combined. I mean, provided that the middle-range value is a sufficient volumetric population density, then we have the potential for over 1000 times that volume, and that's not even touching the largest class of asteroids.
But how constructable would these things be? As I will write about later, there are some valid concerns of stability although they should be manageable. It follows that you work harder against the force of gravitational differentiation when you've "overextended" yourself by making an inner radius a great deal larger than the shell thickness. By looking at the inflated diameter number, you see that that only needs to be true if you require a volume on the scale of what Earth has, which would be a mega-scale engineering problem by its very definition. If you're looking at the middle-range volume requirement, the inner bubble is still relatively small compared with the overall dimension.
Regarding construct-ability, there's also the matter of the pressure before any inflation takes place. This could be a problem by making the center uninhabitable while the atmosphere is produced and supporting infrastructure is built. What is the maximum habitable pressure? I searched around for a few numbers. The compressed air reference points are fairly useless, because the atmosphere would be alien anyway. So given that, the maximum safe SCUBA pressure might be pretty good guidance. Comparing to the above table, it's clear that in order to make Earth volume scales, you will have to learn to deal with impractically high pressure, so it might be an uninhabitable environment to start out with. Thankfully, the pressure declines fairly quickly once the inflation is started, which I wrote about in a previous post.
- trimix suggested 3-4 atm
- compressed air limit 6.4 atm
- recommended diving limit 9.7 atm
- scuba record 31 atm
Ceres is the largest thing in the asteroid belt, and you can see that the distribution function expects just about 1 object at the large diameter values of about 900 km. The fact that my math predicts a diameter of only about 530 km is necessary for creation of Earth atmosphere volume shows that the idea is viable, because that doesn't exhaust all of the available mass. In fact, since Ceres comprises the majority of matter in the asteroid belt, my numbers leave the vast majority of the mass on the table. Ceres would be pretty impossible to break apart, for what it's worth. I calculate its internal pressure to be on the order of 900 atmospheres, which is a higher pressure than our power plant turbines use. This is a very high pressure.
Given some asteroid mass, then provided that it's large, the amount of volume you can obtain by making it into a gravity balloon scales as a 2/3rds power of the diameter. That exponent comes from the fact that a gravity balloon's functional mass-efficiency is a result of the surface area (2) to volume (3) ratio. One consequence of this is that you could actually produce a larger volume from the smaller asteroids by first smashing them into each other and then inflating the resultant body. Ideally, of course, you would just start with a larger asteroid.
What about the moons of the solar system? I've left those out of consideration so far. But to get an ideas of the general abundance of things suitable for a gravity balloon, I looked at what internal pressures you can find in the moons of various planets.
| 0.34 - 0.8 atm | 0.8-30 atm | higher | |
|---|---|---|---|
| Earth | 0 | 0 | 1 |
| Mars | 1 | 0 | 0 |
| Jupiter | 10 | 7 | 5 |
| Saturn | 2 | 2 | 6 |
| Uranus | 14 | 2 | 5 |
| Neptune | 1 | 9 | 3 |
| Total | 28 | 20 | 20 |
There are two major observations here. One, the asteroid belt has a vastly superior population small bodies (it also helps that it's closer to Earth than most planets) that would be good for small gravity balloons. If you wanted Ceres-sized things, however, there are a huge number of moons with absurdly huge internal pressures. It would be extremely difficult to do this in practice, but it's obvious that the matter of moons is easier to get to than that of planets themselves. The volume you could create with these objects goes through the roof.
If you inflated the moon in the simple way that I've written about so far, then you would end up with an object several times larger than the Earth itself (not the atmosphere, the whole thing).